La Charge Cognitive - V. Étude de cas : Le chapitre 'Information Chiffrée'

Nous arrivons à mi-chemin de notre série. Nous avons les outils théoriques :

1. Atomiser pour réduire la difficulté immédiate.
2. Utiliser le visuel (approche type Singapour) pour soutenir la mémoire de travail.
3. Guider la pratique (Exemple résolu → Autonomie) pour consolider.

Mais à quoi cela ressemble-t-il concrètement quand on construit un chapitre entier ?

Prenons un chapitre qui semble anodin mais qui est un véritable champ de mines cognitif en 2nde : Information Chiffrée (Proportions et Évolutions).

Pourquoi est-ce difficile ? Parce que les élèves arrivent avec des intuitions fortes... et souvent fausses ("Une baisse de 50% annule une hausse de 50%", "20% + 30% = 50%"). La charge cognitive ici ne vient pas de la complexité des calculs, mais de la nécessité d'inhiber ces réflexes pour construire un nouveau modèle mental rigoureux.

Voici notre reconstruction "charge cognitive compatible".

Étape 1 : Le Grand Découpage (Atomisation et Spirale)

L'erreur classique est de traiter tout le thème "Pourcentages" en une seule séquence massive de 3 semaines. Pour un novice, mélanger la notion de partie (proportion) et la notion d'évolution (temps) crée une confusion immédiate.

Notre approche consiste à atomiser les compétences en blocs distincts, non seulement pour les clarifier, mais pour les enseigner à des moments différents de l'année.

Le Plan de Bataille

• Bloc A : La Proportion (Vision Statique)

  • Macro-compétence 1 : Identifier l'ensemble de référence (le "Tout") et la sous-population (la "Partie").
  • Macro-compétence 2 : Calculer une proportion et la convertir (Fraction ↔ Décimal ↔ %).
  • Macro-compétence 3 : Inclusion et proportion de proportion (Pourcentage de pourcentage).

• Bloc B : L'Évolution (Vision Dynamique)

  • Macro-compétence 4 : Calculer un taux d'évolution à partir des valeurs (la formule $\dfrac{V_f - V_i}{V_i}$).
  • Macro-compétence 5 : Passer du Taux ($t$) au Coefficient Multiplicateur ($CM$) et inversement. C'est le pivot du chapitre.
  • Macro-compétence 6 : Appliquer une évolution (calculer la valeur finale $V_f$).
  • Macro-compétence 7 : Retrouver une valeur initiale (inverser le CM).

• Bloc C : Les Évolutions Complexes

  • Macro-compétence 8 : Évolutions successives (Produit des CM).
  • Macro-compétence 9 : Évolution réciproque (Inverse du CM).

La Stratégie de la Spirale

Pourquoi ce découpage est-il vital pour la charge cognitive ?

Si vous enseignez les Blocs A, B et C à la suite, la mémoire de travail sature. L'élève confondra "calculer une proportion" (Bloc A) et "calculer un taux d'évolution" (Bloc B), ou "évolution réciproque" (Bloc C) et "retrouver la valeur initiale" (Bloc B).

Une approche efficace consiste à espacer ces blocs (progression spiralée) :

1. Septembre : On traite uniquement le Bloc A (Proportions). On s'assure que c'est acquis.
2. Novembre/Décembre : On introduit le Bloc B (Évolutions). C'est une nouveauté totale. On ne la pollue pas avec les complexités du Bloc C.
3. Mars/Avril : On revient sur le sujet pour traiter le Bloc C. Comme les Blocs A et B sont consolidés en mémoire à long terme, l'élève a les ressources mentales pour comprendre que "l'inverse de +50% n'est pas -50%".

Maintenant que nous avons identifié nos compétences et que nous les avons regroupées en chapitres distincts, intéressons-nous aux supports visuels. Quels schémas pouvons-nous utiliser pour alléger au mieux la charge cognitive, dans l'esprit de la méthode de Singapour ?

Étape 2 : L'Approche Visuelle (Soutenir la mémoire)

L'objectif est d'empêcher l'élève d'additionner les pourcentages ou de se tromper de sens en rendant la structure visible avant d'être calculatoire.

1. Pour la Proportion (Bloc A) : Le Modèle en Barres

Quel est ce schéma ? Il s'agit de représenter le "Tout" par une barre rectangulaire complète, et la "Partie" par une section coloriée de cette barre.

Comment l'utiliser pour alléger la charge ? Au lieu de faire mémoriser la formule abstraite $p = \frac{n_A}{n_E}$, on passe par le dessin.

• Pour une inclusion simple, l'élève voit physiquement que la partie est contenue dans le tout.
• Pour des concepts difficiles comme la proportion de proportion (ex: "Prendre 50% de 40%"), le modèle en barres est souverain.

L'élève dessine la barre des 40%, puis la découpe visuellement pour en prendre 50%. L'opération de multiplication ($0,5 \times 0,4$) ne surgit pas de nulle part : elle devient la traduction symbolique d'un découpage géométrique évident. La mémoire de travail n'a pas à "imaginer" la situation, elle l'a sous les yeux.

2. Pour l'Évolution (Blocs B et C) : Le Schéma "Patates et Flèches"

Quel est ce schéma ? C'est la représentation du lien dynamique entre deux valeurs. On interdit temporairement le signe égal linéaire. On impose :

• Une "patate" de départ ($V_i$) à gauche.
• Une "patate" d'arrivée ($V_f$) à droite.
• Une flèche orientée qui porte l'opérateur $\times CM$.

Application au Bloc B (Évolution simple) :

Ce schéma force l'élève à différencier le statut des nombres. Il distingue instantanément la valeur (dans la patate) de l'opérateur (sur la flèche).

Application au Bloc C (Évolutions complexes) : C'est ici que le schéma révèle toute sa puissance.

• Pour les évolutions successives, on dessine une chaîne : Patate 1 → Patate 2 → Patate 3.

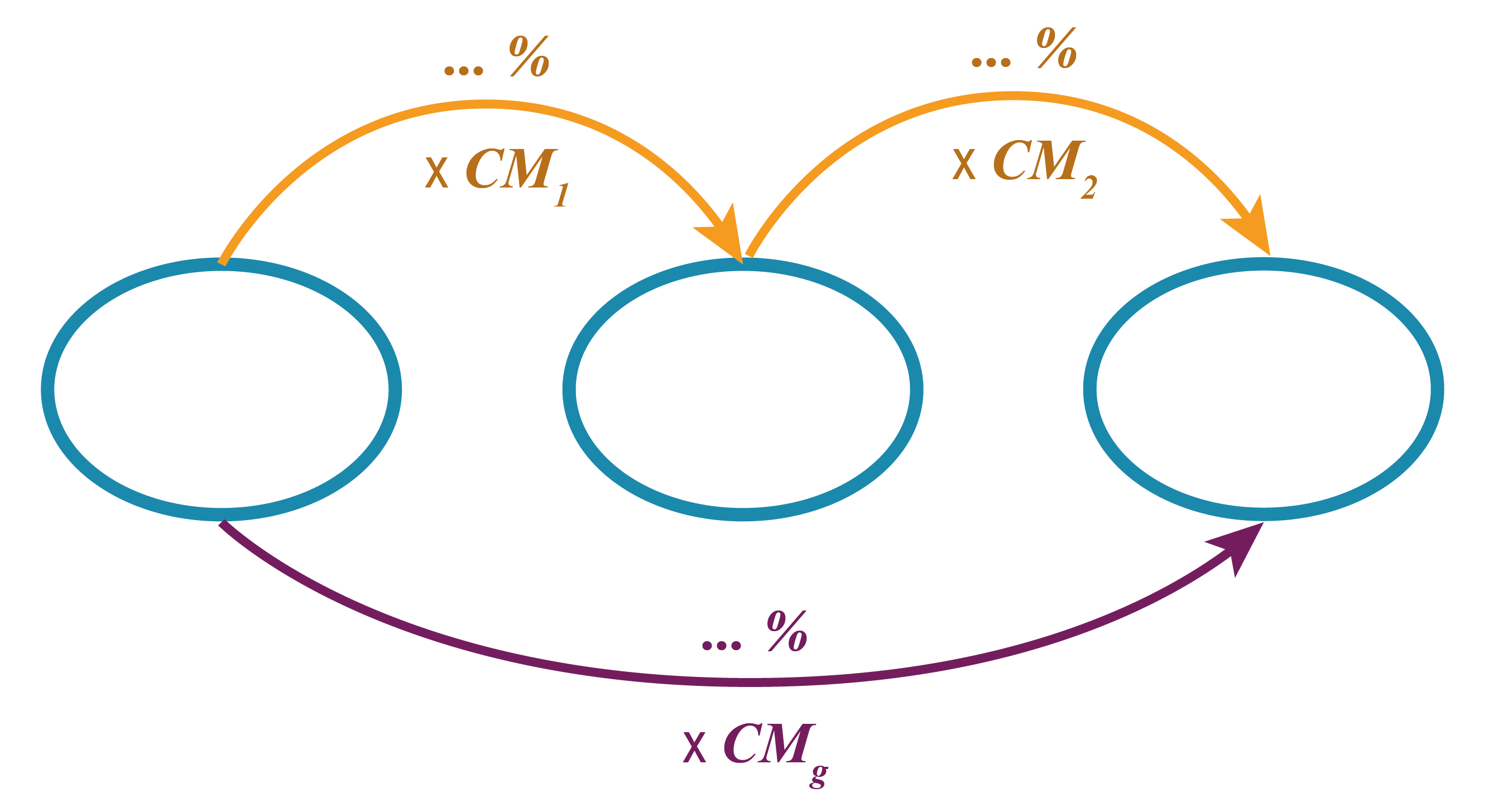
L'élève voit l'enchaînement des opérateurs. Il devient évident qu'on ne peut pas additionner les pourcentages (ce qui reviendrait à sauter les étapes) mais qu'on doit combiner les multiplicateurs.

• Pour l'évolution réciproque, on dessine le chemin aller et on cherche le chemin retour.

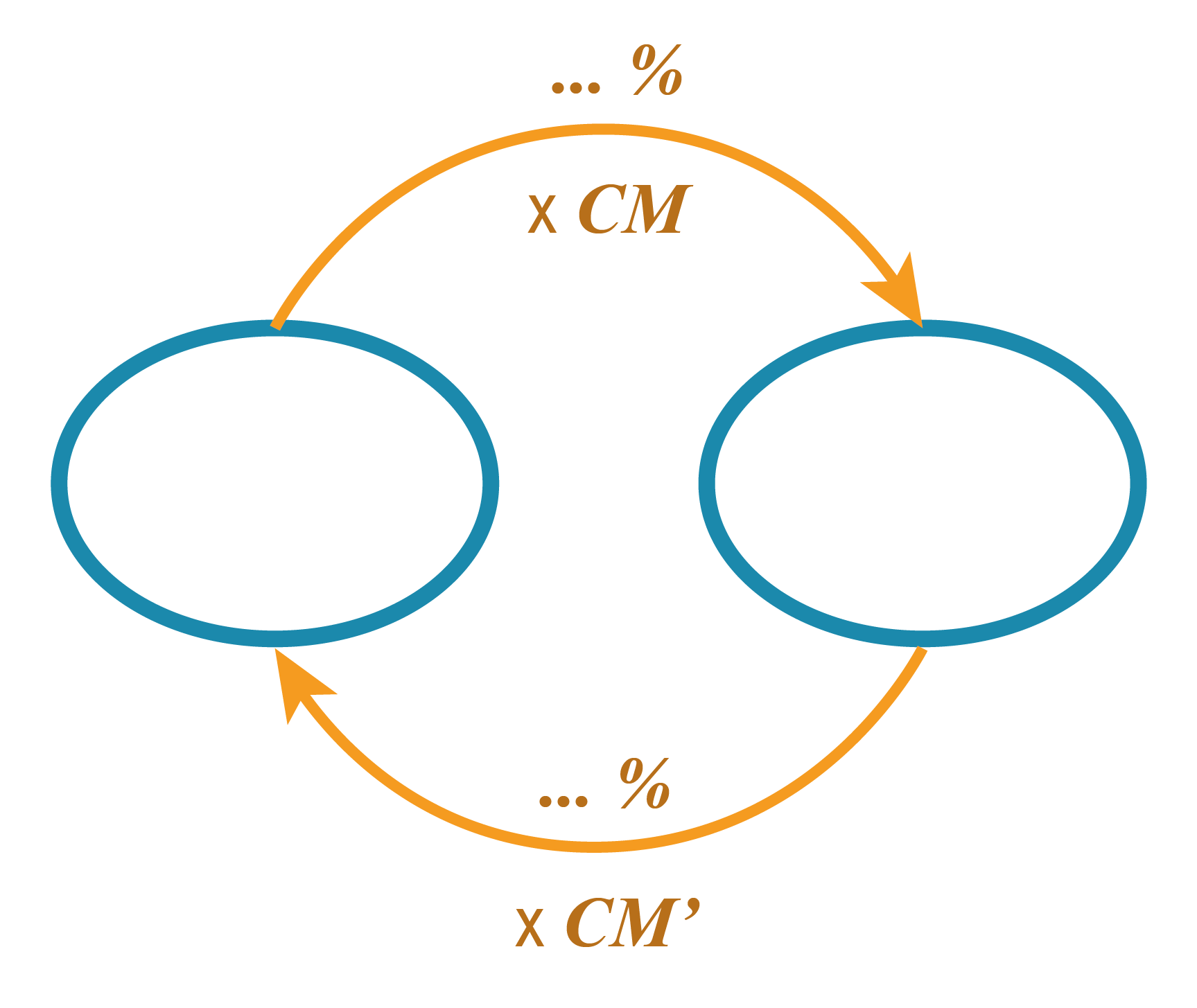
L'élève visualise que le retour n'est pas une simple soustraction du pourcentage, mais l'inverse de la multiplication initiale. Le schéma externe décharge la mémoire de travail de la gestion du "sens" des opérations, permettant de se concentrer sur le calcul.

Nous avons conçu notre cours en nous appuyant sur des modèles visuels (Barres, Patates) pour réduire la charge cognitive lors de la découverte. Mais l'élève ne sait pas encore faire. Il a compris le principe, mais il n'a pas automatisé la procédure. C'est ici que commence la stratégie d'entraînement.

Étape 3 : La Progression des Exercices

Lancer un élève directement sur un problème complexe après le cours est une erreur. Pour respecter la charge cognitive, la phase d'exercices doit elle aussi suivre une progression rigoureuse, à deux niveaux :

1. La granularité : On décompose la "Macro-compétence" (ex: Évolutions successives) en "Micro-compétences" isolées.
2. L'étayage : On fait varier le type d'exercice (Résolu → Guidé → Application → Inversé).

Illustrons cette démarche avec le Bloc C : Les Évolutions Successives.

1. Identifier les Micro-compétences

La "Macro-compétence" est : "Traiter des évolutions successives". Pour l'enseigner, nous l'éclatons en sous-objectifs que l'élève doit valider un par un :

• Micro 1 : Calculer le Coefficient Multiplicateur Global ($CM_G$) à partir des évolutions et le taux d'évolution global.
• Micro 2 : Le piège des évolutions contraires (+X% puis -X%).
• Micro 3 : Passer de deux évolutions à trois ou plus.
• Micro 4 : Retrouver une évolution manquante (Inversion du problème).

2. La mise en musique (Exemples concrets)

Prenons la micro-compétence 1. Voici comment nous agençons les exercices :

Phase A : L'Exemple Résolu (Le Modèle)

Avant de demander à l'élève d'agir, on lui fournit un modèle complet. Sa mémoire de travail est entièrement disponible pour analyser le processus (comment on fait) sans la pression du résultat.

Exemple Résolu :

Un prix subit une hausse de 50 %, suivie d'une baisse de 20 %. Calculer le taux d'évolution global.

Résolution commentée :

1. Je traduis les évolutions en coefficients multiplicateurs (CM).
   • Hausse de +50 % → $CM_1 = 1 + \frac{50}{100} = 1,5$.
   • Baisse de -20 % → $CM_2 = 1 - \frac{20}{100} = 0,8$.
2. J'applique la règle des évolutions successives.
   • Les coefficients se multiplient : $CM_G = CM_1 \times CM_2$.
   • $CM_G = 1,5 \times 0,8 = 1,2$.
3. Je traduis le résultat en pourcentage.
   • $CM_G = 1,2$. Comme c'est supérieur à 1, c'est une hausse.
   • $1,2 - 1 = 0,2$, ce qui correspond à +20 %.

L'élève lit, analyse et comprend la logique.

Phase B : Pratique Guidée (Le Pont)

Maintenant que le modèle est en place, on fait agir l'élève, mais on balise le chemin avec des questions intermédiaires (exercice à trous ou étapes forcées). On reprend la même structure que l'exemple résolu.

Exercice Guidé (Le calcul du CM Global) :

On veut calculer le coefficient multiplicateur (CM) global d'une hausse de 20 % suivie d'une hausse de 30 %.

1. Quel est le CM associé à la première évolution (+20 %) ? (On le note $CM_1$)
2. Quel est le CM associé à la seconde évolution (+30 %) ? (On le note $CM_2$)
3. Quelle opération faut-il faire entre $CM_1$ et $CM_2$ pour trouver le CM global $CM_G$ ?
4. Calculer $CM_G$.

On peut ensuite proposer d'autres exercices guidés en diminuant progressivement le guidage.

Phase C : Pratique d'Automatisation (Fluence)

Maintenant que le concept est compris, il faut automatiser. On propose des exercices plus directs, sans questions intermédiaires, pour libérer de la bande passante mentale.

Exercice d'application directe :

Pour chacun des cas suivants, donner le coefficient multiplicateur global :

a. Une hausse de 8 % suivie d'une hausse de 4 %.

b. Une baisse de 10 % suivie d'une baisse de 10 %.

c. Une baisse de 50 % suivie d'une hausse de 70 %.

Phase D : Piège et complexification

L'élève maîtrise le chemin direct ("Je connais les évolutions, je trouve le global"). On peut s'attaquer maintenant aux pièges usuels, comme la fausse conception fréquente +10% et -10% donnent 0%, en commençant par une approche guidée.

Exercice Guidé (Le Piège) : Un prix subit une hausse de 10 % puis une baisse de 10 %. On veut savoir si le prix final est identique au prix initial.

1. Quel est le $CM_1$ ? Quel est le $CM_2$ ?
2. Calculer le $CM_G = CM_1 \times CM_2$.
3. Le $CM_G$ est-il égal à 1 ?
4. S'agit-il d'une hausse, d'une baisse, ou d'un retour au prix initial ?
5. Quel est le taux d'évolution global (en %) ?

On enchaînera ensuite sur des exercices sans guidage. Une fois le concept compris et les pièges désamorcés, on peut proposer à l'élève des tâches à la charge cognitive plus lourde comme calculer l'évolution globale associée plus de deux évolutions successives, ou celle demandant de manipuler le modèle pour trouver une inconnue comme :

Exercice de Recherche :

Un prix subit une première hausse de 10 %, puis une deuxième évolution $t_2$. L'évolution globale est une hausse de 32 %. Trouver $t_2$ (en %).

Vous pouvez aussi proposer en amont de ces exercices plus lourds, des exercices du même type mais guidés. Mais appliquer ce cycle complet et détaillé (Modèle → Guidé → Fluence → Piège → Expert) pour chaque micro-compétence du programme est un idéal difficile à tenir face à la contrainte de l'emploi du temps.

Cette ingénierie pédagogique doit être vue comme un investissement à cibler en priorité sur les nœuds cognitifs majeurs (ici, typiquement, les évolutions successives et réciproques). Pour le reste, c'est là que réside votre expertise d'enseignant : vous seul pouvez ajuster le curseur du guidage et le nombre d'étapes en fonction du niveau et de l'hétérogénéité de vos élèves.

Résultat

En structurant vos exercices ainsi, vous ne faites pas que "donner des devoirs". Vous construisez un parcours cognitif.

• Le Guidé installe la procédure et corrige les intuitions.
• L'Automatique ancre le savoir en mémoire à long terme.
• Le Problème Inversé vérifie la flexibilité de la connaissance.

C'est cela, un manuel conçu selon la charge cognitive.

En structurant le chapitre ainsi, nous avons transformé des pièges intuitifs en procédures visuelles et logiques. L'élève ne "devine" plus. Il applique un modèle (le schéma fléché) qui guide sa pensée et protège sa mémoire de travail de la surcharge.

Mais attention... même avec le meilleur découpage du monde, si votre support de cours est visuellement saturé ou si vous parlez trop pendant qu'ils lisent, vous saboterez cet apprentissage. C'est ce que nous verrons dans le prochain article.

---

Pour aller plus loin

• Stanislas Dehaene : Ses travaux sur "La bosse des maths" montrent que nous avons une intuition logarithmique des nombres, et que l'intuition des proportions doit être construite contre nos réflexes naturels.
• La théorie des modèles mentaux (Johnson-Laird) : Comprendre, c'est construire un modèle mental de la situation. Nos schémas fléchés sont des "prothèses" pour aider l'élève à construire ce modèle correct.

---